Harmonisation of adjusted calcium equation, is it a realistic aim: a narrative review
Introduction
The establishment of interchangeability (harmonisation) of biochemical test results across laboratories is an essential and important responsibility of laboratory medicine professionals. This is especially true for establishment and running effective clinical networks, where patients may receive laboratory results from multiple laboratory providers within the same network, and hence the availability of valid interchangeable test results is crucial. In the absence of harmonisation, meaningful integration of test results from different laboratory providers into an electronic patient record (EPR) is impossible. Indeed, for the last two decades, there has been a global drive to harmonise all aspects of the laboratory testing processes.
The measurement of serum or plasma calcium is a very commonly requested laboratory test. In serum, around 40% of the calcium is bound to protein (principally albumin), about 10% is complexed with small anions with the remaining (around 50% of the calcium) being in the free ionised form. Although it is only the free ionised calcium that is biologically active, the direct measurement of this fraction is complex and generally not available on high throughput laboratory analysers. In contrast, the measurement of total calcium and albumin is straightforward, and widely available. There has, therefore, been a long-standing considerable interest in the concept of adjusting the serum/plasma calcium concentration to the albumin level to allow for a more accurate assessment of the patient’s calcium status. The practice of reporting ‘adjusted’ calcium alongside total calcium and albumin levels is widely implemented in UK laboratories and across the world. The adjustment equations used to allow this practice, have generally been derived from the linear regression of calcium concentration on albumin concentration (1). There are, however, significant differences between the various reported adjustment equations commonly in use. This variability may clearly relate both to the differences in the analytical techniques employed for calcium/albumin measurements and to the various methods of derivation of the linear regression equation. Additionally, and perhaps more importantly, this variation can be related to the ‘case-mix’ of participants from whom the albumin and calcium results were used to generate the linear regression equations.
Consequently, it is unsurprising to recognise and dissect the evidence for the clinically-significant between-laboratory variation in adjusted-calcium results, which has been reported on a single serum pool (2,3). This variability has the potential to have an adverse impact on clinical outcomes and patient safety. Therefore, there is an urgent need for harmonisation of the whole process of determining and reporting the adjusted calcium levels.
In this article, we discuss the theoretical basis for adjustment of calcium level, we review the different methods for determination of adjusted calcium, the factors contributing to its variability and we explore a number of potential approaches to harmonisation. We present the following article in accordance with the Narrative Review reporting checklist (available at https://jlpm.amegroups.com/article/view/10.21037/jlpm-22-56/rc).
Methods
The focus of this review was assessing the degree of current variation in the calculation, measurement and reporting of adjusted calcium, whether adjusted calcium can potentially be harmonised and what further work may be required to achieve this aim. For this purpose, we performed a search (from the earliest publication date available to January 31, 2022) on the following electronic databases: EMBASE, Medline and PubMed. Search terms covered combinations of expressions used in association with corrected calcium equation (e.g., corrected calcium, adjusted calcium, total calcium, calcium equation, calcium formula, calcium algorithm, albumin adjusted calcium, albumin corrected calcium and protein corrected calcium). We searched for the above term in the abstracts only. The search was restricted to English language publications only and we excluded animal’s studies. The initial search resulted in 141 publications, which included research publication, letters and editorials (Table 1).
Table 1
| Terms | Specifications |
|---|---|
| Date of search | 31 January 2022 |
| Databases and other sources searched | EMBASE and Medline |
| Search terms used | calcium.af AND (total.ti,ab OR serum.ti,ab OR ionised.ti,ab OR ionized.ti,ab) AND (corrected.ti,ab OR correction.ti,ab OR adjust*.ti,ab) AND (equation*.ti,ab OR formula*.ti,ab OR estimation.ti,ab OR algorithm*.af) AND ("comparative stud*" OR "validation stud*" OR "evaluation stud*" OR "intermethod comparison*" OR "case control stud*" OR review*).af; 141 results |
| Timeframe | Earliest publication date available to 31 January, 2022 |
| Inclusion criteria | Human studies, English language only |
| Selection process | The generated list was screened for relevance by N Jassam. The list of ultimately included publications was decided by both authors with no disagreement |
| Any additional considerations, if applicable | Publications for ionised calcium were excluded after the revision for suitability first |
Another search for the analytical technologies and reference interval for albumin and calcium measurement was conducted (e.g., albumin methods, standardisation, calcium method, standardisation) (calcium reference interval, calcium reference range). Restricting the search to English language only, the secondary search resulted in 35 publications. Titles and abstracts were first screened, followed by full text review of relevant studies. Reference lists were also hand searched for potential inclusion. Following the initial screening phase, publications evaluated the full texts to assess their eligibility for inclusion in the review. The publications of interest were classified into the following categories: (I) adjusted calcium concept studies; (II) calcium and albumin methods/performance/standardisation; (III) linearity studies; (IV) calcium reference range studies.
Albumin adjusted calcium—a brief history
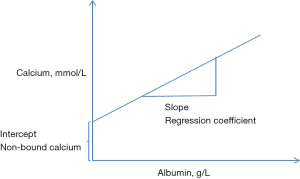
The adjustment of calcium is based on the generation of a regression equation of calcium concentration on albumin concentration (4). This commonly involves the retrieval of albumin and calcium results from a laboratory information system. The regression coefficient of calcium on albumin is then calculated using the intercept from the regression at zero albumin concentration as the non-protein bound calcium (Figure 1).
The adjustment equation is then usually given as:
The mean total calcium was generally taken as the mid-point of the total calcium reference interval, which was 2.40 mmol/L at the time of derivation of Payne’s equation.
This equation is usually re-arranged mathematically to give rise to the most common format of adjusted calcium equation which is:
where ‘derived albumin value’ refers to the albumin concentration around which the calcium will be adjusted.
In the early 1970s, at least three well known equations for the ‘adjustment’ of total calcium for serum albumin were published: Payne et al., 1973 (4), Berry et al., 1973 (5), Orrel, 1971 (6).
The equation generated by Payne, in particular, has been widely used and is given as:
However, it quickly became apparent that different equations gave rise to different values for the adjusted calcium concentration (7).
Sources of variability in adjusted calcium determination
The documented between-laboratory variation in adjusted calcium results (2,3) relates to a number of factors:
- Variation acquired from calcium and albumin measurement;
- Differences between assays in total calcium measurement;
- Differences between assays in albumin measurement.
- Variation built in the method of equation derivation;
- Differences in the derivation of the linear regression equation of calcium on albumin;
- Differences in the albumin concentration range over which adjustment is made.
- Variation intrinsic to the adjusted calcium concept.
- Differences in the case-mix of the population from which the linear regression equation is derived.
We will consider each of these points in turn.
Variation acquired from calcium and albumin measurement
Total calcium measurement
The analytical performance of commercially available and commonly used calcium assays has been widely considered acceptable for various analytical platforms such as Abbott Architect, Roche Modular, Roche Cobas and Artho Vitros (8). In contrast, the Siemens’ calcium assays demonstrated significant concentration dependent bias related to the use of non-commutable calibrator (NIST SRM 915) (9).
Milan’s Model for precision specifications recommended a total acceptable variation for calcium measurements between 0.91–1.36% (10). While there has been a substantial improvement in the imprecision of calcium measurement, it is debatable whether current assays are sufficiently precise for clinical purposes. Using commutable samples, it has been found that total calcium varies by a 3% difference at concentrations <2.20 mmol/L and a 5% difference at concentrations >2.55 mmol/L (3). This finding was further confirmed by other studies, where commutable samples and reference methods were built in the study design. A large calcium total error of 6.5% has been reported, which is exceeding that of acceptable biological variation, across a larger number of various analytical platforms (11,12). Although total calcium has a well-established traceability system, the findings from these studies prompted the authors to call for further optimisation of calcium assays.
The total variation of adjusted calcium is even more pronounced and is significantly wider than that of total calcium. Data from a recent UK audit [2020] showed between laboratories variation of 11%, this is equivalent to a variation of 0.24 and 0.29 mmol/L at the lower and upper limits of the reference range (2.2–2.6 mmol/L) respectively (2).
Albumin measurement
In diagnostic laboratories, serum albumin concentrations are most commonly measured using dye-binding assays, with either Bromocresol Purple (BCP) or Bromocresol Green (BCG). The poor performance of albumin methods is well documented and repeatedly reported as analytically and clinically unsatisfactory (13-15). This has been attributed to a number of factors including a suboptimal standardisation method, between methods imprecision and the poor specificity of BCG methods (15-17).
BCG reacts not only with albumin, but also with α-globulins, haptoglobin and immunoglobulins, resulting in overestimation of albumin concentrations in disease processes that elevate these globulin concentrations in serum. Using albuminaemic commutable samples, BCG method reported results of 14 g/L higher than the nephelometric method results of 0.27 g/L (17).
It has been well recognised that there is significant analytical bias between BCG and BCP methods (15,16). As the difference between albumin methods could be as much as 10 g/L (18). Irrespective of analytical platform, BCG methods in particular, had a larger and more varied mean biases (5–13.9%), with all methods failed to meet the minimum performance criteria for bias based on biological variation limits (2.1%) (19). In one study, the positive bias of BCG methods reduced adjusted calcium concentration by 0.15 mmol/L across the entire range (15). A multi-platform comparative study demonstrated that BCG methods bias is concentration dependent as it varied from 5% at albumin concentration >32 g/L to 10% at albumin concentration <25 g/L (16,18).
In contrast, literature data show that the BCP methods had better selectivity for albumin and less between-methods bias (16). Nonetheless, these BCP methods had their own share of criticism as having been frequently found negatively biased in uremic renal failure patients. However, recent manufactures claim indicated that a new version of BCP, so called the modified BCP (mBCP), do not suffer this uraemia interference (13).
Furthermore, the uncertainty associated with albumin measurement, even after eliminating the bias component, is two times higher than the minimum goal for albumin derived from biological variation model (<2.33%) (20). Although nephelometric-based method and ERM-DA470k/IFCC materials were accepted by the Joint Committee on Traceability in Laboratory Medicine (JCTLM) as a reference measurement system for albumin, albumin standardisation and traceability transfer are still suffering from clinically unacceptable uncertainty and they definitely require further optimisation on an international scale (20,21).
Several studies have confirmed that adjusted calcium is substantially influenced not only by the choice of BCG or BCP methods but also by the specific implementation of a given analytical platform. Subsequently, variability generated from the choice of the albumin method is probably the largest attributing factor to variability in adjusted calcium results. It undoubtedly has implications on the patient’s calcium classification status and has to be regarded as a major source of adjusted calcium variability (16,22).
Variation built in the method of equation derivation
Differences in the derivation of the linear regression equation of calcium on albumin
The fact that adjusted calcium is a mathematical equation based on the regression of albumin on calcium would give rise to multiple sources of variations related to method of calculations, statistics used, analytical and pre-analytical factors.
Different analytical techniques and platforms are available for the measurement of calcium and albumin. Reports demonstrated that the regression coefficients values are influenced by methodology used to measure calcium and albumin (23,24). Barth et al. and Ashby et al. demonstrated differences in regression of calcium on albumin with data collected from different analytical platforms even when the same analytical method had been used (23,25). This difference indicated that variability between local operational protocols and quality indices might partly contributed to the variability of regression coefficient between laboratories (26). This finding has been reproduced world-wide and it was the underlying reason for the recommendation that laboratories derive an equation using their own local platform and methods (27-29).
The most widely used Payne’s adjusted calcium equation, has been calculated using a mid-point of the local calcium reference range 2.2–2.60 mmol/L, that is 2.40 mmol/L (30). This adjusted calcium equation was reproduced by many laboratories world-wide using the same recommended value of 2.40 mmol/L rather than the mid value of the locally derived reference range. Evidence of calcium reference ranges variation exists. Among harmonisation initiatives, the Australian Association of Clinical Biochemistry (AACB) proposed a harmonised calcium reference interval wider than that of the UK Pathology Harmony (31,32). In turn, another UK-based perspective study of 300 healthy individuals from the Yorkshire region, showed that calcium intervals for Abbott Architect, Beckman DXI and Roche were all in good concordance with the UK Pathology Harmony reference interval of 2.2–2.6 mmol/L with the exception of Siemens Advia (2.12–2.51 mmo/L) (33). This difference was attributed to the use of a non-commutable calibrator on Siemens calcium assays (9). Other large national studies, the “Nordic Reference Interval Project (NORIP), the Nationwide Turkish Reference Intervals study and NUMBER reference intervals (Netherlands)” in which harmonisation of measurement methods with commutable calibrator was ensured before the measurement of healthy volunteers samples (34-36). Nevertheless, the reported reference interval for calcium was significantly different from the other initiatives indicating impact of population on reference intervals. Yamamoto and colleagues looked at the impact of population differences across Japan on calcium reference intervals (37). This study recommended a single reference interval for calcium regardless of age or gender differences. On the contrary, Carlsson and colleagues demonstrated higher upper limit for calcium reference interval in a population of 70 years old without cardiovascular disease (CVD) or hyperparathyroidism (38). In conclusion, while there are several initiatives to harmonise the calcium reference range nationally, variations attributed to calibration differences (39), population differences and age exist. Therefore, the mid-point values for calcium reference intervals (Table 2) varies from 2.29–2.45 mmol/L. In no doubt, imposing a value of 2.4 on a population with a lower mid-point value will shift results of adjusted calcium away from the normal range and mask hypocalcaemia. The reverse is true if reference interval mid-point is higher than population mean. It worth mentioning that, while normalising an equation to a fixed value may correct for calibration systemic bias, proportional bias would certainly be overlooked. Therefore, the practice of replacing the use of a local population calcium mean by a fixed value will disregard calibration, methodological and population differences. Imposing a fixed value would also result in a different “derived albumin value” (Eq. [2]) than the actual “population albumin mean”. If the “albumin derived value” in an adjusted calcium equation is not the same as the local “population albumin mean”, the equation will misestimate calcium status in this population (22,39). This concept explains the shortfall of adjusted calcium equations when a common regression model is applied to populations with different albumin means. Example of that; BCG versus BCP (40), different albumin concentrations among different clinical settings, e.g., ambulant versus hospitalised patients (41) and albumin mean difference related to different age groups (42,43).
Table 2
| Study | Calcium interval (mmol/L) | Reference |
|---|---|---|
| Australian adult RI | 2.10–2.60 | Koerbin et al. (31) |
| The Harmony, UK | 2.20–2.60 | Berg et al. (32) |
| Yorkshire RI, UK, Siemens Advia | 2.12–2.51 | Jassam et al. (33) |
| Nordic RI project (NORIP) | 2.17–2.51 | Rustad et al. (34) |
| Turkish nationwide RI Study | 2.12–2.47 | Ozarda et al. (35) |
| NUMBER RI study (Netherlands) | 2.18–2.55 | den Elzena et al. (36) |
| Japan RI harmonisation project | 2.20–2.50 | Yamamoto et al. (37) |
| Reference Intervals for 70-year-old; Abbott Architect | Male: 2.17–2.66; female: 2.18–2.70 | Carlsson et al. (38) |
RI, reference interval.
Many laboratories worldwide use published equation rather than a locally derived one. It’s known that most of the published equations have been derived using BCG albumin methods including Payne’s equation. A recent Australian survey, of the approximately 630 participated laboratories, showed a clear unequal split between the BCP and BCG users. Notably, only 260 were using the BCG dye binding method at the time of that survey. Knowing that albumin concentration can be significantly different between BCG and BCP; this renders the use of published equations inappropriate in most clinical laboratories today and is clearly a major source of inaccuracy. In fact, a recent Australian study showed that Eq. [3] above gave adjusted calcium reference range 2.14–2.67 mmol/L wider and higher than total calcium reference ranges agreed by the ACBB and UK-Pathology Harmony 2.10–2.60 and 2.20–2.60 mmol/L respectively, indicating a possible misestimation of correct calcium status (44). This overestimation of calcium status by the original equation was confirmed by others (24).
The statistical methods of the first generation of calcium equation derivation were all based on the least squares linear regression. Payne, however, argued that the use of Deming regression is a more statistically valid approach (45). Different statistical methods may introduce a small variability in the value of slope and the intercept, and while the difference may not be clinically significant, it certainly adds to the total variation.
The number of data points used to generate regression equations has varied significantly, from one hundred to thousands of data points (1,6,28,41). The number of the data points included may have a statistical impact on the regression value and consequently on the adjusted calcium result generated. This was the underlying reason for the Association of Clinical Biochemistry (ACB-UK) recommendation for a minimum 1,000 data point for equation calculation (46).
Pre-analytical factors are also of importance. Albumin concentration in blood is affected by venous stasis and the prolonged use of tourniquets may alter total calcium concentration due to the rapid increase of protein in the blood sample (47). Equations have differed in their approach to this; for example; Orrel’s but not Payne’s equation excluded data from patients where blood samples were collected with tourniquets (6). Including patient samples with possible venous stasis may partly explain the difference between Payne’s and Orrel’s equations. Therefore, local pre-analytical protocols may affect the quality of data used for the calculation of adjusted calcium equation.
Differences in the albumin concentration range over which adjustment is made
The concept of linear regression of calcium on albumin is based on the assumption of a constant coefficient of calcium binding to albumin at the physiological range 30–50 g/L (48). Outside this range, in particular at a concentration <20 g/L, evidence showed that calcium binding affinity to albumin increases significantly, leading to a higher proportion of hypoalbuminaemic subjects having a calculated adjusted calcium concentration within the healthy population reference interval in spite of having a low ionised calcium concentration (49). The reverse is correct at a concentration >50 g/L with a decrease in the binding affinity of calcium to albumin. There is a broad consensus therefore that it is not acceptable to adjust calcium for albumin concentrations over a threshold of 50 g/L. In contrast, there is no agreement on the lower threshold. A number of studies recommended linearity range of 30–50 and 32–50 g/L, below which the regression of calcium to albumin is not constant (25,49). Barth et al., however, statistically proved that linearity relationship of calcium to albumin can be extended to 16–50 g/L (23). Some laboratories have made pragmatic recommendations for a wider linearity range of albumin concentrations (10–50 g/L, local data) and this approach has been endorsed by others (50). In practice, there are differences between laboratories in the albumin concentration range over which adjustment is made, a difference that would contribute to the overall variability in adjusted calcium determination.
This lack of agreement on a harmonised linear range of the calcium adjustment is further complicated by different methods for albumin measurement. Almost all linearity studies established the relationship between calcium and albumin were measured by the BCG method, including Payne’s equation, with the exception of Smith et al, in which the BCP method has been used (51). Therefore, confirmatory studies in particular with BCP albumin methods are required.
Variation intrinsic to the adjusted calcium concept
Differences in the case-mix of the population from which the linear regression equation is derived
Since its inception, adjusted calcium equation has been widely criticised (52,53). The albumin adjusted calcium concept was deemed suitable for clinical practice based on the assumption of no intra-individual variability in the binding affinity of albumin to calcium (54). This assumption was challenged, as a considerable intra-individual variation has been found (55,56). Individual regression factors have been reported to vary in health between 0.013 and 0.044 and this variation is expected to be more pronounced in disease. This variation has been reported to be statistically and clinically significant. Moreover, several reports demonstrated that the regression coefficients values are influenced by the population from which the equation is derived, e.g., various patient groups (45), age (paediatric, adult, elderly). Weaving et al. demonstrated that albumin concentrations change with age. The authors challenged the concept of using a single regression factor to adjust calcium for various age groups (57,58). The use of an adjusted calcium has been questioned in critically ill patients (53,59), cancer patients (60), renal failure patients; pre-dialysis (61) and end stage renal failure (62,63). A study by Payne suggested that the regression of total calcium on albumin may also differ in the pregnant population and in menopause (64-66). This illustrates the potential influence of population differences and patient mix on the adjustment equation, which would render the application of a common regression coefficient to different populations and clinical settings a source of inaccuracy. Literature evidence showed that an equation derived from dialysis patients and applied to them outperformed the conventional adjusted calcium equation (67). The poor performance of adjusted calcium equations has prompted attempts to modify existing equation by inclusion of a population specific parameter; such as the inclusion of phosphate in equations for renal failure patients (68). Another attempt showed an equation derived from/and applied to ambulant patients compared well with ionised calcium and performed better than Payne’s equation (41). These studies introduce a new practice, which is called “A population specific equation”, a concept that requires further exploration, nonetheless emphasizes the importance of case-mix on the adjusted calcium equation performance.
There is ample evidence in the literature demonstrating the limitations of the current format of adjusted calcium equation. Nevertheless, adjusted calcium remains in use due to the lack of a practical replacement and pragmatically due to the ease of its measurement and familiarity with its interpretation.
The way forward
Table 3 presents factors affecting adjusted calcium results. It is important that the causes of variability in adjusted calcium are identified, addressed and eliminated if possible. Considering that standardising adjusted calcium equations is not currently attainable without eliminating the albumin and calcium calibration issues, minimising other sources of variability is the only possible way forward at this point of time. Drawing on knowledge of two initiatives for harmonisation of adjusted calcium by the ACB-UK and the AACB-Australia; we conclude that a similar approach is required until the equivalence of results produced for calcium and albumin is assured by a high metrological standardisation system.
Table 3
| Variables | Factors contributing to adjusted calcium variability |
|---|---|
| Calcium | Methods: Arsenazo III, CPC, NM-PABTA |
| Method traceability | |
| Analytical performance | |
| Reference interval | |
| Albumin | Methods: BCG vs. BCP |
| Method traceability | |
| Analytical performance and method selectivity | |
| Age and gender | |
| Data collection and sifting criteria and equation derivation | Payne’s equation vs. other equations |
| Inclusion and exclusion criteria | |
| Statistical method for equation derivation | |
| Population | Hospitalised vs. ambulant population |
| Children, adult and elderly | |
| Various patient groups and case mix |
CPC, cresolphthalein complexone; NM-PABTA, 5-nitro-5’-methyl-(1,2-bis (o-aminophenoxy) ethan-N, N, N’, N’-tetraacetic acid. BCG, Bromocresol Green; BCP, Bromocresol Purple.
For example, due to the problematic standardisation of albumin methods, coupled with the widespread use of the poor specificity BCG assay, the AACB recommended that laboratories adopt the dye binding BCP method as their routine method of choice. The AACB also recommended no harmonisation for the albumin reference interval at this stage (69). Considering that, the use of assay specific reference interval is a safer practice as the current harmonised reference interval for albumin may mislead users away from the concentration difference between these methods. In the context of adjusted calcium, the use of a single and a more specific method such as the BCP will be the right move for achieving interchangeable results for adjusted calcium.
Finally, the large number of variables in the adjusted calcium derivation process makes it important that all steps of the process included in the derivation of the adjusted calcium equation are considered and described in sufficient details to laboratories professionals to fully understand the equation derivation method. Indeed, that was what the ACB-UK attempted in 2015. With the aim to reduce variability in adjusted calcium reporting, the ACB-UK produced guidelines for standardising the adjusted calcium equation calculation (46). The guidelines described the method of equation calculation, recommended a minimum data point (1,000 data point at least) to be used for equation derivation and specified the siftings criteria for post data collection handling with a national recommendation for laboratories to locally derive and monitor the performance of their own equation. Up-to-date, no national audit has been performed to demonstrate the impact of these guidelines on the adjusted calcium variability. A final note; it is premature to embrace a common reference interval for adjusted calcium without further optimisation for albumin and calcium method standardisations, hence the UK Harmony and the AACB, recommended that the adjusted calcium reference interval should be the same as the total calcium.
These initiatives demonstrate that harmonisation of adjusted calcium measurements is a consideration, but further work is needed. International professional bodies such as the International Federation of Clinical Chemistry and Laboratory Medicine (IFCC) and the European Federation of Laboratory Medicine (EFLM) are in a good place to lead on production of a consensus document and drive further optimisation of the standardisation of both calcium and albumin methods. Though adjusted calcium is an old practice, there is a great role for education to disseminate knowledge about its limitations and opportunities to improve its practice. Table 4 gives recommendations for adjusted calcium harmonisation for consideration of readers, researchers, diagnostic companies and professional bodies.
Table 4
| No. | Recommendation | Further work |
|---|---|---|
| 1 | Laboratories continue to derive their own equation | Descriptive guidelines cover the whole process from data collection to method of calculation |
| 2 | Agree a linearity range for albumin on calcium regression | Studies for BCP linearity range assessed preferably against ionised calcium are required |
| 3 | Promote the use of the modified-BCP method | Professional bodies: to promote the profile of the modified-BCP method in a similar manner to that used to raise the profile of the enzymatic creatinine assay |
| Diagnostic companies: to improve the standardisation and precision of albumin and calcium methods | ||
| 4 | Harmonisation of calcium reference interval | Systematic review for calcium reference intervals in the view of harmonisation |
| 5 | To explore the age-related adjusted calcium equation and population specific adjusted calcium | Further confirmatory work is required |
BCP, Bromocresol Purple.
Conclusions
The accuracy of adjusted calcium results affected by several variables collectively lead to significant variation in adjusted calcium measurement. Therefore, accurate reporting and classification of calcium status requires a unified approach for the derivation of the equation, consensus over the linearity range applied, and standardisation of the measurements of albumin and calcium. Confirmatory studies are required for linearity of the range over which adjustment is made. However, the clinical relevance of albumin method on adjusted calcium cannot be overstated. Unless the lack of specificity and poor standardisation of albumin methods issue is resolved, harmonisation of adjusted calcium is hard to achieve.
Acknowledgments
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the editorial office, Journal of Laboratory and Precision Medicine for the series “Calcium Adjustment in Laboratory Medicine”. The article has undergone external peer review.
Reporting Checklist: The authors have completed the Narrative Review reporting checklist. Available at https://jlpm.amegroups.com/article/view/10.21037/jlpm-22-56/rc
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at https://jlpm.amegroups.com/article/view/10.21037/jlpm-22-56/coif). The series “Calcium Adjustment in Laboratory Medicine” was commissioned by the editorial office without any funding or sponsorship. NJ served as the unpaid Guest Editor of the series and serves as an unpaid editorial board member of Journal of Laboratory and Precision Medicine from October 2021 to September 2023. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Payne RB, Carver ME, Morgan DB. Interpretation of serum total calcium: effects of adjustment for albumin concentration on frequency of abnormal values and on detection of change in the individual. J Clin Pathol 1979;32:56-60. [Crossref] [PubMed]
- Jassam N, Thomas A, Hayden K, et al. The impact of the analytical performance specifications of calcium and albumin on adjusted calcium. Ann Clin Biochem 2020;57:382-8. [Crossref] [PubMed]
- Koerbin G, Tate JR, Ryan J, et al. Bias Assessment of General Chemistry Analytes using Commutable Samples. Clin Biochem Rev 2014;35:203-11. [PubMed]
- Payne RB, Little AJ, Williams RB, et al. Interpretation of serum calcium in patients with abnormal serum proteins. Br Med J 1973;4:643-6. [Crossref] [PubMed]
- Berry EM, Gupta MM, Turner SJ, et al. Variation in plasma calcium with induced changes in plasma specific gravity, total protein, and albumin. Br Med J 1973;4:640-3. [Crossref] [PubMed]
- Orrell DH. Albumin as an aid to the interpretation of serum calcium. Clin Chim Acta 1971;35:483-9. [Crossref] [PubMed]
- Sanderson C. Correction of serum calcium measurements. Br Med J 1974;1:245. [Crossref]
- Van Houcke SK, Rustad P, Stepman HC, et al. Calcium, magnesium, albumin, and total protein measurement in serum as assessed with 20 fresh-frozen single-donation sera. Clin Chem 2012;58:1597-9. [Crossref] [PubMed]
- Perich C, Ricós C, Alvarez V, et al. External quality assurance programs as a tool for verifying standardization of measurement procedures: Pilot collaboration in Europe. Clin Chim Acta 2014;432:82-9. [Crossref] [PubMed]
- Braga F, Panteghini M. Performance specifications for measurement uncertainty of common biochemical measurands according to Milan models. Clin Chem Lab Med 2021; Epub ahead of print. [Crossref] [PubMed]
- Jansen R, Jassam N, Thomas A, et al. A category 1 EQA scheme for comparison of laboratory performance and method performance: An international pilot study in the framework of the Calibration 2000 project. Clin Chim Acta 2014;432:90-8. [Crossref] [PubMed]
- Weykamp C, Secchiero S, Plebani M, et al. Analytical performance of 17 general chemistry analytes across countries and across manufacturers in the INPUtS project of EQA organizers in Italy, the Netherlands, Portugal, United Kingdom and Spain. Clin Chem Lab Med 2017;55:203-11. [Crossref] [PubMed]
- Ueno T, Hirayama S, Sugihara M, et al. The bromocresol green assay, but not the modified bromocresol purple assay, overestimates the serum albumin concentration in nephrotic syndrome through reaction with α2-macroglobulin. Ann Clin Biochem 2016;53:97-105. [Crossref] [PubMed]
- Ueno T, Hirayama S, Ito M, et al. Albumin concentration determined by the modified bromocresol purple method is superior to that by the bromocresol green method for assessing nutritional status in malnourished patients with inflammation. Ann Clin Biochem 2013;50:576-84. [Crossref] [PubMed]
- Infusino I, Braga F, Mozzi R, et al. Is the accuracy of serum albumin measurements suitable for clinical application of the test? Clin Chim Acta 2011;412:791-2. [Crossref] [PubMed]
- Bachmann LM, Yu M, Boyd JC, et al. State of Harmonization of 24 Serum Albumin Measurement Procedures and Implications for Medical Decisions. Clin Chem 2017;63:770-9. [Crossref] [PubMed]
- van Schrojenstein Lantman M, van de Logt AE, Thelen M, et al. Serum albumin measurement in nephrology: room for improvement. Nephrol Dial Transplant 2022;37:1792-9. [Crossref] [PubMed]
- Carfray A, Patel K, Whitaker P, et al. Albumin as an outcome measure in haemodialysis in patients: the effect of variation in assay method. Nephrol Dial Transplant 2000;15:1819-22. [Crossref] [PubMed]
- European Federation of Laboratory medicine (EFLM) Biological Variation database. Available online: https://biologicalvariation.eu/ [accessed June 2022].
- Infusino I, Panteghini M. Serum albumin: accuracy and clinical use. Clin Chim Acta 2013;419:15-8. [Crossref] [PubMed]
- Zegers I, Keller T, Schreiber W, et al. Characterization of the new serum protein reference material ERM-DA470k/IFCC: value assignment by immunoassay. Clin Chem 2010;56:1880-8. [Crossref] [PubMed]
- Jassam N, Narayanan D, Turnock D, et al. The effect of different analytical platforms and methods on the performance of population-specific adjusted calcium equation. Ann Clin Biochem 2020;57:300-11. [Crossref] [PubMed]
- Barth JH, Fiddy JB, Payne RB. Adjustment of serum total calcium for albumin concentration: effects of non-linearity and of regression differences between laboratories. Ann Clin Biochem 1996;33:55-8. [Crossref] [PubMed]
- Mohd Ariffin ZA, Jamaluddin FA. Albumin adjusted calcium: Study in a tertiary care hospital. Malays J Pathol 2020;42:395-400. [PubMed]
- Ashby JP, Wright DJ, Rinsler MG. The adjusted serum calcium concept--a reappraisal. Ann Clin Biochem 1986;23:533-7. [Crossref] [PubMed]
- Davies SL, Hill C, Bailey LM, et al. The impact of calcium assay change on a local adjusted calcium equation. Ann Clin Biochem 2016;53:292-4. [Crossref] [PubMed]
- Pawade YR, Ghangale SS, Dahake HS. Albumin-adjusted calcium: are previously published regression equations reliable for your laboratory? – a pilot study. Int J Med Sci Public Health 2013;2:217-22. [Crossref]
- James MT, Zhang J, Lyon AW, et al. Derivation and internal validation of an equation for albumin-adjusted calcium. BMC Clin Pathol 2008;8:12. [Crossref] [PubMed]
- Ridefelt P, Helmersson-Karlqvist J. Albumin adjustment of total calcium does not improve the estimation of calcium status. Scand J Clin Lab Invest 2017;77:442-7. [Crossref] [PubMed]
- Payne RB. Clinical interpretation of population-specific adjusted calcium values. Ann Clin Biochem 2022;59:381-2. [Crossref] [PubMed]
- Koerbin G, Cavanaugh JA, Potter JM, et al. 'Aussie normals': an a priori study to develop clinical chemistry reference intervals in a healthy Australian population. Pathology 2015;47:138-44. Erratum in: Pathology 2015 Jun;47(4):396. [Crossref] [PubMed]
- Berg J, Lane V. Pathology Harmony; a pragmatic and scientific approach to unfounded variation in the clinical laboratory. Ann Clin Biochem 2011;48:195-7. [Crossref] [PubMed]
- Jassam N, Luvai A, Narayanan D, et al. Albumin and calcium reference interval using healthy individuals and a data-mining approach. Ann Clin Biochem 2020;57:373-81. [Crossref] [PubMed]
- Rustad P, Felding P, Lahti A, et al. Proposal for guidelines to establish common biological reference intervals in large geographical areas for biochemical quantities measured frequently in serum and plasma. Clin Chem Lab Med 2004;42:783-91. [Crossref] [PubMed]
- Ozarda Y, Ichihara K, Aslan D, et al. A multicenter nationwide reference intervals study for common biochemical analytes in Turkey using Abbott analyzers. Clin Chem Lab Med 2014;52:1823-33. [Crossref] [PubMed]
- den Elzen WPJ, Brouwer N, Thelen MH, et al. NUMBER: standardized reference intervals in the Netherlands using a 'big data' approach. Clin Chem Lab Med 2018;57:42-56. [Crossref] [PubMed]
- Yamamoto Y, Hosogaya S, Osawa S, et al. Nationwide multicenter study aimed at the establishment of common reference intervals for standardized clinical laboratory tests in Japan. Clin Chem Lab Med 2013;51:1663-72. [Crossref] [PubMed]
- Carlsson L, Lind L, Larsson A. Reference values for 27 clinical chemistry tests in 70-year-old males and females. Gerontology 2010;56:259-65. [Crossref] [PubMed]
- Weaving G. Calcium - An adjustment too far or not far enough? Ann Clin Biochem 2020;57:401-3. [Crossref] [PubMed]
- Kato A, Takita T, Furuhashi M, et al. Influence of the assay for measuring serum albumin on corrected total calcium in chronic hemodialysis patients. Ther Apher Dial 2011;15:540-6. [Crossref] [PubMed]
- Jassam N, Hayden K, Dearman R, et al. Prospective study comparing the outcome of a population-specific adjusted calcium equation to ionized calcium. Ann Clin Biochem 2020;57:316-24. [Crossref] [PubMed]
- Jassam N, Gopaul S, McShane P, et al. Calcium adjustment equations in neonates and children. Ann Clin Biochem 2012;49:352-8. [Crossref] [PubMed]
- Sorva A, Elfving S, Pohja P, et al. Assessment of calcaemic status in geriatric hospital patients: serum ionized calcium versus albumin-adjusted total calcium. Scand J Clin Lab Invest 1988;48:489-94. [Crossref] [PubMed]
- Hughes D, Koerbin G, Potter JM, et al. Harmonising Reference Intervals for Three Calculated Parameters used in Clinical Chemistry. Clin Biochem Rev 2016;37:105-11. [PubMed]
- Payne RB. Calculation of slope by Deming's method from least-squares regression coefficients and imprecision. Clin Chem 1984;30:807. [Crossref] [PubMed]
- O’Kane, M, Jassam, N, Barth, JH, et al. Albumin-adjusted calcium: a position paper. The Association of Clinical Biochemistry and Laboratory Medicine 2015. Available online: http://www.acb.org.uk/docs/defaultsource/committees/clinical-practice/guidelines/acb-adjusted-calcium-position-paper-march-2015.pdf?sfvrsn=2 [accessed 1 April 2022]
- Renoe BW, McDonald JM, Ladenson JH. The effects of stasis with and without exercise on free calcium, various cations, and related parameters. Clin Chim Acta 1980;103:91-100. [Crossref] [PubMed]
- Besarab A, DeGuzman A, Swanson JW. Effect of albumin and free calcium concentrations on calcium binding in vitro. J Clin Pathol 1981;34:1361-7. [Crossref] [PubMed]
- Besarab A, Caro JF. Increased absolute calcium binding to albumin in hypoalbuminaemia. J Clin Pathol 1981;34:1368-74. [Crossref] [PubMed]
- Payne RB. Albumin-Adjusted Calcium and Ionized Calcium. Clin Chem 2019;65:705-6. [Crossref] [PubMed]
- Smith JD, Wilson S, Schneider HG. Misclassification of Calcium Status Based on Albumin-Adjusted Calcium: Studies in a Tertiary Hospital Setting. Clin Chem 2018;64:1713-22. [Crossref] [PubMed]
- Ladenson JH, Lewis JW, Boyd JC. Failure of total calcium corrected for protein, albumin, and pH to correctly assess free calcium status. J Clin Endocrinol Metab 1978;46:986-93. [Crossref] [PubMed]
- Dickerson RN, Alexander KH, Minard G, et al. Accuracy of methods to estimate ionized and "corrected" serum calcium concentrations in critically ill multiple trauma patients receiving specialized nutrition support. JPEN J Parenter Enteral Nutr 2004;28:133-41. [Crossref] [PubMed]
- Pain RW, Rowland KM, Phillips PJ, et al. Current "corrected" calcium concept challenged. Br Med J 1975;4:617-9. [Crossref] [PubMed]
- Phillips PJ, Pain RW, Hartley TF, et al. Current "corrected" calcium concept rechallenged. Clin Chem 1977;23:1938-9. [Crossref] [PubMed]
- Ryan GD, Masarei JR. Validity of "corrected" calcium values. Clin Chim Acta 1979;91:329-35. [Crossref] [PubMed]
- Weaving G, Batstone GF, Jones RG. Age and sex variation in serum albumin concentration: an observational study. Ann Clin Biochem 2016;53:106-11. [Crossref] [PubMed]
- Pfitzenmeyer P, Martin I, d'Athis P, et al. A new formula for correction of total calcium level into ionized serum calcium values in very elderly hospitalized patients. Arch Gerontol Geriatr 2007;45:151-7. [Crossref] [PubMed]
- Slomp J, van der Voort PH, Gerritsen RT, et al. Albumin-adjusted calcium is not suitable for diagnosis of hyper- and hypocalcemia in the critically ill. Crit Care Med 2003;31:1389-93. [Crossref] [PubMed]
- Ijaz A, Mehmood T, Qureshi AH, et al. Estimation of ionized calcium, total calcium and albumin corrected calcium for the diagnosis of hypercalcaemia of malignancy. J Coll Physicians Surg Pak 2006;16:49-52. [PubMed]
- Gauci C, Moranne O, Fouqueray B, et al. Pitfalls of measuring total blood calcium in patients with CKD. J Am Soc Nephrol 2008;19:1592-8. [Crossref] [PubMed]
- Clase CM, Norman GL, Beecroft ML, et al. Albumin-corrected calcium and ionized calcium in stable haemodialysis patients. Nephrol Dial Transplant 2000;15:1841-6. [Crossref] [PubMed]
- Jain A, Bhayana S, Vlasschaert M, et al. A formula to predict corrected calcium in haemodialysis patients. Nephrol Dial Transplant 2008;23:2884-8. [Crossref] [PubMed]
- Payne RB, Little AJ, Evans RT. Albumin-adjusted calcium concentration in serum increases during normal pregnancy. Clin Chem 1990;36:142-4. [Crossref] [PubMed]
- Payne RB, Barth JH. Adjustment of serum total calcium for albumin concentration: values change with age in women but not in men. Ann Clin Biochem 1996;33:59-62. [Crossref] [PubMed]
- Nordin BE, Need AG, Hartley TF, et al. Improved method for calculating calcium fractions in plasma: reference values and effect of menopause. Clin Chem 1989;35:14-7. [Crossref] [PubMed]
- Obi Y, Nguyen DV, Streja E, et al. Development and Validation of a Novel Laboratory-Specific Correction Equation for Total Serum Calcium and Its Association With Mortality Among Hemodialysis Patients. J Bone Miner Res 2017;32:549-59. [Crossref] [PubMed]
- Ferrari P, Singer R, Agarwal A, et al. Serum phosphate is an important determinant of corrected serum calcium in end-stage kidney disease. Nephrology (Carlton) 2009;14:383-8. [Crossref] [PubMed]
- Koerbin G, Sikaris K, Jones GRD, et al. An update report on the harmonization of adult reference intervals in Australasia. Clin Chem Lab Med 2018;57:38-41. [Crossref] [PubMed]
Cite this article as: Jassam N, O’Kane M. Harmonisation of adjusted calcium equation, is it a realistic aim: a narrative review. J Lab Precis Med 2023;8:8.