
Understanding and expressing variation in measurement results
Introduction
“The times they are a-changin” from the error—concepts where the true value is claimed to be known (1,2) to measurement uncertainty as a subjective state of mind, “doubt about the true value of the measurand that remains after making a measurement” (3). When philosophical matters take center stage in such drastic changes, getting to grips with the agreed and straightforward practical procedures used to summarize measurement results (4-7) is pertinent. Even on this secure ground, debates remain on using (normal) distribution-based or data-driven, distribution-independent methods and sum-of-squares or absolute differences to calculate variation. This paper aims to elucidate such matters from theoretical and practical perspectives.
As the name implies, statistics were originally about “state data”, using information obtained from population samples to predict the characteristics of the entire population. The population perspective still holds its ground to the sample perspective especially in mathematical statistics and epidemiological research. Statistics are commonly defined as “the branch of the scientific method that deals with the data obtained by counting or measuring the properties of populations” (8). Distribution-independent, data-driven measures are, however, finding increased use. When a particular probability distribution, e.g., the normal distribution, is chosen as a fundamental theoretical paradigm, straightforward, solid theoretical conclusions can be made based on mathematics and probability theory. Therefore, theoretical mathematical statistics are commonly favored over the handling of natural study results since clear conclusions are possible based on the chosen theoretical models. It is, for example, far more unequivocal to base models on unadulterated normal-distribution theory rather than on actual results adulterated, e.g., by bias.
Early natural scientists such as A.M. Legendre (9,10), F.W. Bessel (11), and W.F.R. Weldon (12-15) were essential in re-focusing normal-distribution-dependent statistical theories to various real-world data (16). They pointed out a path on the rocky road of real data that is still fruitful, for example, in the natural sciences. Currently used statistical procedures are essential in the industry and technical aspects of medicine, including Laboratory Medicine. The focus then is, e.g., on validation and verification of measurement procedures (17), handling traceability of results (18), lot-to-lot variability (19), and practical statistical quality control (17) rather than on inference focusing on a hypothetical “population” (20). Central to such evaluation are descriptions of central tendency and variation, including variance component analysis using methods that frequently do not assume a normal distribution of the results.
The core properties of the commonly used measures of central tendency, variation, and inference, such as degrees of freedom and handling bias, are still subject to debate. Since results in biomedicine are frequently not normally distributed (21), biased, and include outliers; it is vital to understand the fundamentals, strengths, and limits of normal distribution-based methods and their alternatives (22-24).
Measures of central tendency
The arithmetic mean
Surprisingly, given its ubiquitous use, the arithmetic mean has a history as recent as the seventeenth century (7,9,25-27). In antiquity, the Greeks realized the advantage of pooling results, but they adhered to the common notion that “the best results” should count, thus favoring the most common result (25)—the mode. Eisenhart uniquely describes the history of introducing the arithmetic mean (5,7,28). Characteristics of the arithmetic mean are that it is the “center of gravity” of the measurement results and, together with the standard deviation (SD), one of the two parameters of the normal distribution. Importantly, it is very much influenced by the presence of extreme results (Figure 1).

The median
The median is the middle result in a series of ranked results, i.e., the 0.5th quantile. There are an equal number of results above and below it. Notably, the median differs from the midpoint of the range of the results. Therefore, the range and interquartile range (IQR) are commonly asymmetric around the median. The median is uniquely found as the single middle result when the number of observations is odd and the average of the two middle results when the number is even. It is a good index of the central tendency since it is not influenced by a few very high or low results, including outliers.
Bias
Measurement trueness is the “closeness of agreement between the average of an infinite number of replicate measured quantity values and a reference quantity value” (30,31). Measurement trueness is inversely related to the ratio scale quantity “measurement bias” (31,32), a constant deviation inherent in every measurement of a measurand in a sequence of measurements repeated over shorter or longer periods. Measurements can be corrected for bias if the magnitude and direction of the bias are known. In the high-volume practice of laboratory medicine, the correction for bias is theoretically and practically challenging and, therefore, rarely comprehensively practiced except in the Netherlands.
Measures of variation
The variance and the SD
The least squares method was jointly discovered in standardization work leading to the metric system by A.M. Legendre (10,33) and in astronomy by C.F. Gauss (10,33). Legendre published the method in 1805 and Gauss in 1809, the latter showing its inherent relation to the normal distribution (9,34).
Imprecision expressed as SD summarizes the average Euclidean distance between the measurement results along the measurement scale in a single figure. Figure 2A shows six measurement results of pipetting 200 microliters of water using a worn-out automatic pipette. The results are shown along a matrix’s X and Y axis, and all differences between a specific result and all the other results are calculated and squared. Each comparison consists of a difference between two values, free to vary, except when a result is compared to itself. Each comparison between a specific result and all the other results in the group adds two “degrees of freedom” to the total degrees of freedom, as shown in the DF column. Importantly, when a result is compared to itself, there are no additions to the degrees of freedom or the sum of squares since a value compared to itself never has the chance of contributing to the overall variation.
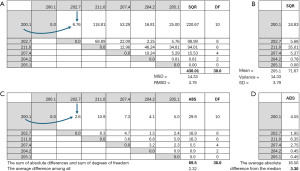
The SQR column shows the sum of squares of the differences for each row, and the total sum of squares of the differences and the total degrees of freedom are shown at the bottom of the columns.
When the sum of squares 430.01 is divided by the degrees of freedom 30, it results in the variance 14.3337, which is identical to Eq. [2], the formula calculating the estimated variance of the population using data from a random sample from the population.
When the variance and SD are calculated in this way, the results are identical to those obtained with Eqs. [2] and [3], the equations commonly used to calculate the variance and SD as variations around the arithmetic mean value. The sum of squared differences can be calculated between any value and the results, but the total sum of squares will be lowest if and only if the value is the arithmetic mean value, as shown in Eq. [2].
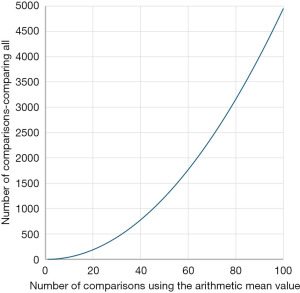
The number of comparisons needed when using the method depicted in Figure 2A increases exponentially with the number of data [n(n − 1)/2] (Figure 3), in contrast with the number of comparisons needed when the arithmetic mean value is used (Figure 2B, Eq. [2]) where the increase is linear.
The number of degrees of freedom is estimated quite differently in the example depicted in Figure 2B when the arithmetic mean is estimated as the first step. Since all results have already been entered into the arithmetic mean calculation, the arithmetic mean value restrains the degrees of freedom to one less than the total number of results. Thus, if the number of results and the arithmetic mean are known, any result from the group of results can be found, provided the other results are known. This also illustrates the logic of the Bessel (35) correction (n−1) when calculating the sample variance.
The mean squared difference (MSD), variance, respective root mean squared difference (RMSD), and SD calculated by the methods depicted in Figure 2A,2B will give identical results irrespective of the probability distribution of the results or the possible presence of bias. There is, therefore, no reason to use the more laborious method depicted in Figure 2A instead of the commonly used method shown in Figure 2B. Despite the close theoretical connection between the arithmetic mean and the SD on the one hand and the normal distribution on the other, it is crucial to understand that the “non-identical twin” of SD, the RMSD, is relevant irrespective of the distribution of the results and in the presence of bias. However, reporting the SD means that the results are not influenced by bias.
The RMSD and SD are fundamentally a mathematical expression of the mean distance of each result along the measurement scale from every other result and the arithmetic mean.
Willmott and Matsuura have observed that the RMSE varies with the variability of the differences between results, the square root of the number of deviations, and the average difference (36), making a case for measures of variation that do not square the differences since squaring emphasizes the influence of the most prominent differences.
Moments
Karl Pearson taught engineering before concentrating on statistical work. He originated the use of the engineering (mechanics) concept “moment” to describe the characteristics of the normal distribution (13,15). In mechanics, the moment expresses a lever force about the point around which it turns. The first moment is the arithmetic mean, the second is the variance, the third is a measure of skewness, and the fourth is a measure of peakedness, the kurtosis.
SD population estimated by SD sample
In a Gresham lecture on January 31st, 1893, Karl Pearson (37) proposed a re-defined concept and term “standard deviation” instead of the RMSD primarily used at that time (9,13,38,39). He defined SD as the square root of the average of the squared deviations taken from the arithmetic mean of the population distribution (39). It was also taken from the sample arithmetic mean when the population arithmetic mean is unknown. The SD, as defined by Karl Pearson, and indirectly earlier also by Gauss, remains a preferred measure of variation since it is a parameter in the normal distribution and essential as a standard effect size, e.g., according to Guide to the Expression of Uncertainty in Measurement (GUM) (40).
Importantly, Pearson’s SD estimates the population SD for normal-distribution-based statistical inference rather than a distribution-independent description of the sample results (a role still played by the RMSD). This association of the “SD” with the normal distribution implies that it should not include bias. Systematic error components should be eliminated before the SD is calculated and used for statistical inference. In contrast, bias and imprecision are natural and legitimate in analyzing variance components and other descriptive statistical procedures that do not assume normal distribution of the population results.
The squaring of differences has several pros and cons:
Pros:
- It always results in a positive value;
- The sum of squared deviations of two or more independent (orthogonal) causes of variation stands for the total variation described by the Pythagorean theorem. Therefore, variances add, and SDs do not add components of variation;
- If the population is normally distributed, the SD varies least among the available sample parameters describing variation.
Cons:
- The square root must be used to return the measure of variation to its original unit;
- Squaring emphasizes the most prominent differences between results.
Calculating and presenting the traditional SD and relative SD (commonly called coefficient of variation, CV or CV%) means a risk of losing the intuitive interpretation of the values because sums-of-squares-based measures vary in response to the central tendency and variability (41). Both influence the CV%, and both the SD and the arithmetic mean are therefore needed to understand which of the two are most influential in a particular case. Therefore, absolute-error or absolute-deviation-based measures are increasingly used, e.g., in climatology, where understanding by the public is paramount (36,41,42). However, they are unlikely to replace the standard and relative SD in metrology and laboratory medicine soon.
The relative SD (CV, CV%)
It is challenging to compare the variation of measurement results obtained on different parts of the measurement scale since the SD varies correspondingly. For example, comparing the SD of a new 10-microliter pipette to that of a new 1,000-microliter pipette results in an order of magnitude more prominent SD for the latter even though the variability is similar. Therefore, expressing the variation relative to the arithmetic mean as the relative SD/coefficient of variation is commonly advantageous.
The standard error of the mean (SEM)
The SEM is the sample estimate of the SD of the mean of numerous samples taken from the population.
The SEM is always smaller than the SD. Already at n=16 the SEM is only a quarter of the SD. The SE illustrates possible differences in mean values when making statistical inferences (41), but is not an optimal measure of variation as such since it estimates the variation of the arithmetic mean value and not the variation in the results themselves.
Degrees of freedom
The degree of freedom (42,43) is the number of results in the final calculation of a statistic that are free to vary. Several approaches to explaining degrees of freedom have been proposed (44-47). The oldest one, attributed to Bessel (42) (the Bessel correction), is easiest to understand.
Repeatability imprecision expresses the average distance between all repeated measurement results of the same sample during a run/day. The difference between all measurement results is calculated and squared by arranging them on a matrix’s X- and Y-axes (Figure 2). Two measurement results are entered into each comparison. Both are subject to variation. It is evident from the outset that all measurement results will be compared to themselves once in each round of comparisons and, therefore, will not contribute to the overall sum of squares once in each round since the difference between two identical results is always zero. This explanation corresponds to Cramérs mathematical explanation of degrees of freedom as “The rank of a quadratic form” (48). Suppose the mean is used, the far more efficient method for calculating the variance and SD (Figure 3). In that case, the Bessel correction (n−1) is used for the sample estimate of the population variance and SD.
Bessel’s correction also reflects the degrees of freedom of the residuals (the difference between the individual results and the arithmetic mean). While there are n independent results in the sample, there are only n−1 independent residuals since the sum of residuals is, by definition, 0. When the mean and n−1 of the sample results are known, the last result is given/fixed—it has no degree of freedom.
A parameter is a numerical statement about the entire population of interest. Parameters are impossible to measure without uncertainty. However, each parameter has a corresponding statistic that can be measured by taking a random sample from the population. A sample statistic is calculated from the results measured from the sample. It is a numerical statement about the sample that can be made, reflecting the population’s corresponding parameter (SD in this case). Sample estimates of parameters are based on different amounts of information. The number of independent pieces of information that enter the sample estimate of a parameter is the degrees of freedom. In general, the degrees of freedom of a sample are equal to the number of independent results that go into the estimate minus the number of statistics estimated as steps in the sample estimation of the parameter itself. For example, suppose the variance will be estimated from a random sample of n independent results. In that case, the degree of freedom equals the number of independent results (n) minus the statistic estimated as an intermediate step (one − the arithmetic mean) and is therefore equal to n−1.
Wikipedia offers a thorough mathematical proof of the Bessel’s correction.
The C4 correction
It is well known that the expected value of the population variance with the n-estimate shown in Eq. [2] is biased. It is much less known that Eq. [3] with the supposedly unbiased n−1 estimate remains biased because of the square root transformation from a variance estimate to a SD estimate of the variation (22). The Jensen’s inequality explains the root cause of this bias. The square root is a concave function resulting in the expected value of the SD being less than or equal to the square root of the expected value of the squared deviations (i.e., the variance) (which constitutes the Jensen’s inequality). The property of being unbiased is preserved only by linear operations. Therefore, an unbiased estimator’s square or the square root will be biased. Additionally, those unbiased estimators for the variance and SD, which depend upon bias correction factors, are unbiased only if the probability distribution function for the data is Gaussian.
The underestimation of the population SD may be of minor practical significance since it has already decreased to about 3% at n=10. However, low numbers of replicates are common, for example, in experimental sciences and when determining preliminary control limits in quality control. The C4 correction is therefore emphasized in advanced quality control texts (49,50).
The C4 (or the Helmert distribution) enables the calculation of the unbiased expected value of the population’s SD by an N-dependent increase of the sample estimate using the gamma function Γ() (49,51), see Eqs. [7] and [8].
Expressed in MS Excel formula it is “=EXP(GAMMALN(N/2)+LN(SQRT(2/(N-1)))-GAMMALN((N-1)/2))” (Table 1).
Table 1
| N | C4 | % underestimation |
|---|---|---|
| 2 | 0.79788 | 20.21 |
| 3 | 0.88623 | 11.38 |
| 4 | 0.92132 | 7.87 |
| 5 | 0.93999 | 6.00 |
| 6 | 0.95153 | 4.85 |
| 7 | 0.95937 | 4.06 |
| 8 | 0.96503 | 3.50 |
| 9 | 0.96931 | 3.07 |
| 10 | 0.97266 | 2.73 |
The mathematical statistics behind this is that the sample SD follows a scaled chi distribution. Therefore, the correction factor is the mean of the chi distribution.
A mathematically simpler approximation is obtained by replacing n−1 in the Bessel’s correction with n−1.5.
The range
The range is the difference between the largest and smallest results. It is easily estimated when the results are ranked. Still, it is not an optimal measure of the variation since the two extreme results decide the range independently of the remaining results. Furthermore, the range increases not only with increased variation of the results but also with an increase in the number of results. It is, therefore, impossible to estimate how much of the range is attributable to variation in the population and how much is due to the number of results.
Mean absolute deviation (MAD) and similar measures
The acronym “MAD” measures variation using several definitions detailed below.
The mean absolute difference is the mean absolute difference between by all results in the sample without using any reference or measure of central tendency (Figure 2C).
The mean absolute deviation (MAD) (eq. [9]) or mean absolute distance (MAD) [sometimes called “average absolute deviation” (AAD)] is the mean of the absolute deviation from a measure of central tendency, which can be the arithmetic mean, the median, or the mode. Alternatively, the deviation can be measured from a reference value.
The absolute deviations increase linearly with the increase in the variation and are therefore intuitive. The differences between the individual and expected results are positive, negative, or zero, but the absolute function turns them into a positive Euclidean distance.
For the normal distribution, the MAD, calculated using the mean as the measure of central tendency, is about 0.8× SD (Eq. [10]).
Whether RMSE or MAD is the least biased and most robust measure of measurement uncertainty in the environmental sciences (36,52-56) is still being debated (57). Studies of results with several distributions have only shown minor distribution-related differences.
Suppose the mean absolute distance is chosen as measured by all results in the sample without using a reference or measure of central tendency. In that case, care should be taken to reduce the degrees of freedom (Bessel correction) when comparing a result with itself, as shown in Figure 2C and as pointed out by Charlier (58,59). This also compensates for the underestimate of the sample estimate of the variation in the population.
Tests for normality
The Anderson-Darling test (60,61) has been recommended for use in laboratory medicine when determining reference intervals (62). Other tests for normality are available (63) in commonly used programs for statistical analysis with Shapiro-Wilk test having similar favorable properties for medical laboratory data as Anderson-Darling test (63).
Quantiles
Quantiles are non-parametric statistics that divide results into groups, each containing predetermined fractions. Their properties are directly related to the original results but not to any theoretical distribution, so they can be used for any data distribution. Quantiles maintain their properties and identities under the transformation of results, resulting in a direct correspondence between the percentage points of the original and transformed results.
When a collection of results is to be described by quantiles, the first step is to arrange them in order of size (rank). A quantile is a location measure/statistic which divides the ranked observations into two parts. The part below the quantile contains the quantile portion of the observations with the lowest rank numbers. Thus, the 0.25 quantile cuts off the lowest 25% of the observations with the lowest rank numbers from the rest. Consequently, observations with higher rank numbers are above the quantile (Table 2).
Table 2
| Quantile | Cuts off a portion of the observations |
|---|---|
| Range | 1.0×n (all results) |
| Median | 0.5×n (half of the results) |
| Quartile | 0.25×n (n=1, 2, 3, 4) |
| Decile | 0.1×n (n=1, 2,..., 10) |
| Centile/percentile | 0.01×n (n=1, 2,..., 100) |
The number of results in the sample from the population is expressed as n.
Methods for calculating quantiles
The methods used to calculate quantiles depend on the purpose. If the purpose is to estimate the population quantiles from the sample, e.g., when estimating reference intervals, several sample results are needed since health workers must be confident that the reference interval represents the population (64,65). However, we also need methods to estimate quantiles of other, even small, group results, e.g., to describe the central tendency of few results in experimental work.
A fundamental idea behind the calculation of quantiles is that, for example, if xi is the ith largest observation and it is precisely measured in a sample from a continuous distribution, the proportion of the distribution less than xi is i/(n+1), on average, when the sample size is n. Thus, the quantiles divide up the population into n+1 pieces, each, on average, having probability 1/(n+1).
Methods to be used when the goal is to estimate population quantiles from the sample values
Parametric or non-parametric methods may both be used to estimate population quantiles. Parametric estimation techniques require that data fit a specified distribution type (usually Gaussian) or that such a distribution is approximated by applying a transforming function to the data [e.g., using logarithms of the measured values or the Box-Cox transformation (66)]. Parametric estimates of population quantiles are theoretically more precise with smaller sample sizes than those obtained by non-parametric methods, provided the assumption of distribution type is valid. The question, however, about whether an observed distribution (or its transform) conforms to the Gaussian form adds to the uncertainty of the estimates.
When estimating population quantiles from a sample of n results, rank the values described below and multiply (n+1) by the quantile. N+1 rather than n is used because it can be shown that n+1 provides an unbiased estimate of a quantile. It is obvious that the population estimate of quantiles, e.g., quantiles enclosing the IQR (multiplying the quantile value with n+1), is always more expansive than the IQR of the sample (multiplying with n). For a non-integer rank number, interpolation is necessary to find the quantile value (67,68).
The q- and (1-q)-quantiles are only estimable if q is above 1/n. This means that when determining the reference limits, the 0.025 and 0.975 quantiles require at least 40 results since 1/40=0.025 (64). If N=120, the 2.5 percentile corresponds to rank 3 (0.025×121), and the 97.5 percentile corresponds to rank 118 (0.975×121). This means the two lowest reference values are below the 2.5 percentile (rank 3), and the two highest reference values are above the 97.5 percentile (rank 118). This is the reason for recommending 120 reference values for deciding nonparametric reference intervals, as at least 120 reference values are needed to avoid the effect of the two lowest and two highest values, thus eliminating extreme results.
When the goal is to summarize the results of an experiment, n is used instead of n+1 when calculating quantiles (67). Rank the n values by arranging them in order of magnitude, giving the smallest value the rank number 1 and the highest value the rank number n. Consecutive rank numbers should be assigned to two or more equal values (ties). The rank number R(q) of the quantile Q(q) is found in the following manner: R(q) = (n × q)+0.5, where q is the fraction of the data values to be contained in the quantile and n is the number of results. If R(q) is an integer, an estimation of Q(q) is straightforward since a single rank and sample value correspond to the Q(q). If R(q), on the other hand, is not an integer, the quantile Q(q) lies between the sample values with ranks next to R(q). If the ranked values have ties and R(q) falls on or between the ranks of tied values, Q(q) is the same as these tied results, provided the number of such ties is insignificant compared with the sample size. Equal unit intervals are associated with each rank; that from 0.5 to 1.5 is associated with rank 1, that from 1.5 to 2.5 with rank 2, and so on. The total length from, for example, 0.5 to 10.5 is 10 units. One-quarter of 10 is 2.5. To find the sample Q(0.25) we mark points 2.5 units apart starting at 0.5. Thus 0.5+2.5=3.0. This gives the position of the first quartile, Q1.
When the number of results is even
It is already mentioned that when the number of results is even, we must interpolate to estimate the median as the average of the two middle observations. Other quantiles may also fall between observations, which means that some convention is needed to give them a unique value. Three commonly used interpolation methods are described below.
The “average of ranks” method aligns with the method used to estimate the median when the number of observations is even. For example, if the rank number of the quantile R(q) is 3.75 then the quantile is the average of the values with the rank numbers 3 and 4. However, it may be argued that the quantile value in this case should lie closer to the value of rank 4 than rank 3, which brings about the need for other interpolation methods.
The “weighing fraction/linear interpolation” method states that the quantile will be the value of the lower rank plus the difference between the values of the higher and the lower ranks times the non-integer part of the rank number of the wanted quantile. For example, if R(q) is 3.75 and R(3) and R(4) represent the value of the numbers ranked number 3 and 4, respectively, then the quantile value will be: Q(q) = R(3) + [R(4) − R(3)] × 0.75
The “proportional interpolation” method states that the quantile will be the sum of the value of the lower rank times the non-integer part of the rank number of the wanted quantile and the value of the higher rank times one minus the non-integer part of the rank number of the wanted quantile. In the above example this means: Q(q) = R(3) × 0.75 + R(4) × (1−0.75).
There are no objective grounds for advocating one of the above three methods rather than the others. The “weighing fraction/linear interpolation” method is most widely used. However, when reporting results, the research worker must declare which interpolation method he has used when calculating quantiles if the data are few, and the interpolation method used may significantly influence the reported statistic.
Expressing quantiles as descriptive statistics
Readers of biomedical research communications are accustomed to seeing results described as, e.g., 12±2, where 12 is the arithmetic mean, and two can be either the SD or the SEM. The SD and the SEM are always symmetric around the mean, meaning that a single number is sufficient to indicate variation. Quantile values are not necessarily symmetric around the median, meaning that descriptive statistics based on quantiles cannot be written as compact as parametric descriptive statistics. Furthermore, there is no agreement in the literature about how quantile descriptive statistics should be depicted in print, a fact that may have favored parametric descriptive statistics. The quantiles should be written as 14:11–17 where 14 is the median, and 11 and 17 are the lower and upper quartiles (68).
Quantiles commonly used for summarizing data
Any quantile values can be used to describe variations in results and can be chosen depending on the context. Traditionally, however, the interval of the central half of the data, the IQR, is commonly used for describing research results, and the quantiles 0.025 and 0.975 for describing reference intervals. Extreme values much less influence the IQR than they influence the range. Given that there are 40–120 results, the IQR is a reproducible measure of the variation of the population results—the more numerous results, of course, the better.
Parametric versus nonparametric descriptive statistics
Phenomena caused by many independent factors are commonly distributed according to the normal distribution (69). Suppose we have good reasons to believe that specific measurement results are normally distributed; there is no better way of describing the data than reporting the mean and the SD because these two statistics define the normal distribution. Furthermore, we add the knowledge that the data are distributed according to the normal distribution of the information in the results. On the other hand, if parametric statistics are calculated when the data are non-normal, the arithmetic mean and the SD risk distorting the information value of the results.
The quantiles are commonly seen as non-parametric statistics, even though they can be determined either by parametric or non-parametric methods. Their validity does not depend on assumptions about the form of the distribution that generated the observations, which makes them applicable in all circumstances. Many critical sample- and population properties can be represented in quantiles. From a mathematical statistics viewpoint, all available information about the sample may be given by the values of the quantiles. A valuable property of quantiles is keeping their identity under a continuous monotonic variable transformation. Thus, after transformation, there will be a direct correspondence between the percentage points of the original sample and those of the transformed sample. The mean and SD, on the other hand, do not keep their identity under transformation.
Knowledge about the mean and SD of the transformed sample is challenging to interpret in terms of the statistics of the original sample and vice versa, even if there are formulas for adjusting for many transformations.
Resampling methods
The results obtained by repeated measurements of a sample under repeatability conditions are the best information about the central tendency and variation in the population unless further independent information about the probability distribution is available. Numerous resampling of the actual results with replacement provide estimates of parameters of interest and their uncertainties, such as the arithmetic mean, the median, and the quartiles (70-72).
Uncertainty and uncertainty components
The repeatability uncertainty of measurement results is expressed quantitatively as the dispersion characteristics of the results under constant conditions (30). The reproducibility uncertainty also includes the uncertainty due to changing conditions, such as between days, between lots, between laboratories, etc. (73).
Imprecision profiles
Variation commonly is not consistent along the measurement interval. Imprecision profiles (74-76) should therefore be evaluated and handled appropriately (74), especially at concentrations important for diagnoses.
Standard score
The normal distribution is tabulated with the arithmetic mean of 0 and a SD of 1. The reason is that all values in normal distributions can be converted to this standard normal score using standard scores or z-scores. In equation x, the arithmetic mean is the sample estimate of the population arithmetic mean, and the SD is the sample estimate of the population SD.
The standard score expresses the number of SDs a result differs from the arithmetic mean of its group. It provides a probabilistic measure of such a value by referring to a standard normal distribution with a mean 0 and a SD of 1. In other words, it is the number of SDs the value of a raw score is above or below the mean value of what is being measured.
Sums-of-squares-based measures of variation
Sums-of-squares measures are generally preferred for calculating and expressing components of variation. A primary reason for this is that components of imprecision are additive as squared quantities, they are historically well-established, and they facilitate the calculation of ratios, which enable the partitioning of bias components.
The CLSI guideline EP15 (77) is commonly used for the verification of measurement procedures. It is recommended that a stabilized control sample be measured in five replicates on five subsequent days. The within- and between-days SDs are then calculated to calculate the total SD for establishing quality control limits.
The control limits for measurement procedures are usually revised, especially in out-of-control situations, using several days of results from the analysis of stabilized control samples. The number of control results available each day commonly varies in this situation, prompting the need for modified procedures for calculating the total SD, considering the unbalanced variance component analysis (78,79).
Absolute-value-based measures of variation
The public commonly misinterprets the characteristics of the RMSE, and MAD is, therefore, increasingly used in the climatic literature (36,54,80). The probabilistic and formal logical proofs of Hodson’s review (57) are impeccable concerning normally distributed data and data distributed according to the Laplace distribution. However, the strongest arguments of Willmott & Matsuura (36) are neither based on probabilistic theory nor formal logic. They address how the public optimally interprets information in central tendency, variation, and statistical inference measures. There is communication value in using measures/parameters that are most likely to convey the most thorough understanding of the actual phenomenon/mechanism.
Absolute-value-based components of variation have only recently been described, enabling partition into the following components (I) bias deviations, (II) proportionality deviations, and (III) unsystematic deviations (53,81).
Conclusions
Medical laboratories extensively use measures of central tendency and variation in measurement results to establish and monitor bias and measurement uncertainty, e.g., to determine whether analytical performance specifications (APS) and goals for internal and external quality control are met. The arithmetic mean, SD, CV% and z-score are commonly used for the purpose, supported by a long-standing tradition, guidelines, standards and regulators. Laboratories commonly struggle with a high prevalence of false positive rejection of internal quality control results which for example may be due bias due to lot-number changes or to non-normal distribution of the results. It is therefore time for a critical overview of the measures of central tendency and variation used in medical laboratories making room e.g., for distribution-independent measures, and measures which cater for mixtures of bias and random variation causing measurement uncertainty. A start could for example be to consider using the abbreviation RMSD instead of SD when the results risk being influenced by bias, and to use an agreed version of MAD for the expression APS.
Acknowledgments
Funding: None.
Footnote
Peer Review File: Available at https://jlpm.amegroups.com/article/view/10.21037/jlpm-24-53/prf
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at https://jlpm.amegroups.com/article/view/10.21037/jlpm-24-53/coif). E.T. serves as an unpaid editorial board member of Journal of Laboratory and Precision Medicine from April 2024 to March 2026. E.T. received a grant from The County Council of Östergötland to his institution and Royalty for the textbook Laurells Klinisk Kemi i Praktisk Medicin to himself. He also received consulting fees from Nordic Biomarker. The author has no other conflicts of interest to declare.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Bich W. From Errors to Probability Density Functions. Evolution of the Concept of Measurement Uncertainty. IEEE Transactions on Instrumentation and Measurement 2012;61:2153-9. [Crossref]
- Bich W. Error, uncertainty and probability. Metrology and Physical Constants 2013;185:47-73.
- Bich W. A proposed new definition of measurement uncertainty. Ukrainian Metrological Journal 2023:3-6.
- Eisenhart C. Laws of Error-II: The Gaussian Distribution. In: Kotz S, Read CB, Balakrishnan N, et al. editors. Encyclopedia of Statistical Sciences. Hoboken, New Jersey: Wiley Online Library; 2006:4068-82.
- Eisenhart C. Laws of Error-I: Development of the Concept. In: Kotz S, Read CB, Balakrishnan N, et al. editors. Encyclopedia of Statistical Sciences. Hoboken, New Jersey: Wiley Online Library; 2006:4052-68.
- Eisenhart C. Laws of Error-III: Later (Non-Gaussian) Distributions. In: Kotz S, Read CB, Balakrishnan N, et al. editors. Encyclopedia of Statistical Sciences. Hoboken, New Jersey: Wiley Online Library; 2006:4083-6.
- Raper S. The shock of the mean. Significance 2017;14:12-7. [Crossref]
- Kendall MG, Stuart A, Ord JK, et al. Kendall's advanced theory of statistics. 6th ed. London, New York: Edward Arnold, Halsted Press; 1994.
- Stigler SM. The history of statistics. The measurement of uncertainity before 1900. Cambridge, Massachusetts: The Belknap Press of Harvard University Press; 1986.
- Stigler SM. Statistics and the Question of Standards. J Res Natl Inst Stand Technol 1996;101:779-89. [Crossref] [PubMed]
- Lawrynowicz K. Friedrich Wilhelm Bessel. Basel: Birkhäuser verlag; 1995.
- Pence CH. ‘‘Describing our whole experience’’: The statistical philosophies of W. F. R. Weldon and Karl Pearson. Studies in History and Philosophy of Biological and Biomedical Sciences 2011;42:475-85. [Crossref] [PubMed]
- Magnello ME. Karl Pearson's Gresham lectures: W. F. R. Weldon, speciation and the origins of Pearsonian statistics. Br J Hist Sci 1996;29:43-63. [Crossref] [PubMed]
- Porter TM. Karl Pearson: the scientific life in a statistical age. Princeton, NJ; Oxford: Princeton University Press; 2004.
- Magnello ME. Karl Pearson and the Establishment of Mathematical Statistics. International Statistical Review 2009;77:3-29. [Crossref]
- Stigler SM. Statistics on the table: the history of statistical concepts and methods. Cambridge: Harvard University Press; 1999.
- Theodorsson E. Validation and verification of measurement methods in clinical chemistry. Bioanalysis 2012;4:305-20. [Crossref] [PubMed]
- Panteghini M. An improved implementation of metrological traceability concepts is needed to benefit from standardization of laboratory results. Clin Chem Lab Med 2024; Epub ahead of print. [Crossref] [PubMed]
- Loh TP, Markus C, Tan CH, et al. Lot-to-lot variation and verification. Clin Chem Lab Med 2023;61:769-76. [Crossref] [PubMed]
- van Schrojenstein LM. How measurement uncertainty impedes clinical decision-making, https://hdl.handle.net/2066/311846: Radboud University; 2024.
- Mar JC. The rise of the distributions: why non-normality is important for understanding the transcriptome and beyond. Biophys Rev 2019;11:89-94. [Crossref] [PubMed]
- Deming WE. Some theory of sampling. Wiley publications in statistics. New York: Wiley; 1950.
- Lehmann EL, Casella G. Theory of point estimation. 2nd ed. Springer texts in statistics. New York: Springer; 1998.
- Chernick MR. Bootstrap methods: a guide for practitioners and researchers. 2nd ed. Wiley series in probability and statistics. Hoboken: Wiley-Interscience; 2008.
- Stigler SM. The seven pillars of statistical wisdom. Cambridge: Harvard University Press; 2016.
- Stahl S. The evolution of the normal distribution. Mathematics Magazine 2006;7:96-113. [Crossref]
- Stigler SM. The history of statistics: the measurement of uncertainty before 1900. Cambridge: Belknap Press of Harvard University Press; 1986.
- Simpson T. On the Advantage of Taking the Mean of a Number of Observations, in Practical Astronomy. Philos Trans R Soc 1756;49:82-3.
- Cotes R. Logometria. In: Gowing R, editor. Roger Cotes - Natural Philosopher. Cambridge: Cambridge University Press; 1722.
- JCGM. International vocabulary of metrology—Basic and general concepts and associated terms (VIM 3). Bureau International des Poids et Mesures. 2012. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf, accessed April 8th, 2019.
- ISO. ISO 5725-1:2003 Accuracy (trueness and precision) of measurement methods and results: Part 1: General principles and definitions. Technical Committee: ISO/TC 69/SC 6 Measurement methods and results. Geneva, Switzerland: International Organization for Standardization; 2003.
- Theodorsson E, Magnusson B, Leito I. Bias in clinical chemistry. Bioanalysis 2014;6:2855-75. [Crossref] [PubMed]
- Eisenhart C. The meaning of "least" in least squares. J Wash Acad Sci 1964;54:24-33.
- Sheynin OB. Gauss, C.F. And the Theory of Errors. Archive for History of Exact Sciences 1979;20:21-72. [Crossref]
- Lawrynowicz K. Friedrich Wilhelm Bessel 1784-1846. Basel: Birkhäuser Verlag; 1995.
- Willmott CJ, Matsuura K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Climate Research 2005;30:79-82. [Crossref]
- Porter TM. The rise of statistical thinking: 1820-1900. Princeton; Guildford: Princeton University Press; 1986.
- Pearson ES. Studies in the History of Probability and Statistics. XIV Some Incidents in the Early History of Biometry and Statistics, 1890-94. Biometrika 1965;52:3-18. [Crossref] [PubMed]
- Pearson K. Contributions to the mathemathical theory of evolution. Philosophical Transactions of the Royal Society of London A (1887-1895) 1894;185:71-110.
- JCGM. Evaluation of measurement data—Guide to the expression of uncertainty in measurement. JCGM 100:2008, GUM 1995 with minor corrections. Available online: http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf. Joint Committee for Guides in Metrology; 2008.
- Lee DK, In J, Lee S. Standard deviation and standard error of the mean. Korean J Anesthesiol 2015;68:220-3. [Crossref] [PubMed]
- Student. The probable error of a mean. Biometrika 1908;6:1-25. [Crossref]
- Fisher RA. On the Interpretation of χ2 from Contingency Tables, and the Calculation of P. Journal of the Royal Statistical Society 1922;85:87-94. [Crossref]
- Rodgers JL. Degrees of Freedom at the Start of the Second 100 Years: A Pedagogical Treatise. Advances in Methods and Practices in Psychological Science 2019;2:396-405. [Crossref]
- Eisenhauer JG. Degrees of Freedom. Teaching Statistics 2008;30:75-8. [Crossref]
- Pandey S, Bright CL. What Are Degrees of Freedom? Social Work Research 2008;32:119-28. [Crossref]
- Good IJ. What Are Degrees of Freedom? The American Statistician 1973;27:227-8. [Crossref]
- Cramér H. Mathematical methods of statistics. Princeton, New Jersey: Princeton University Press; 1945.
- Wheeler DJ. Advanced Topics in Statistical Process Control. The power of Shewhart’s Charts. Knoxville: SPC Press, Inc.; 1995.
- Duncan AJ. Quality Control and Industrial Statistics. Homewood, Illinois: Irwin; 1986.
- Gurland J, Tripathi RC. A Simple Approximation for Unbiased Estimation of the Standard Deviation. The American Statistician 1971;25:30-2. [Crossref]
- Brassington GB. Forecast Errors, Goodness, and Verification in Ocean Forecasting. Journal of Marine Research 2017;75:403-33. [Crossref]
- Robeson SM, Willmott CJ. Decomposition of the mean absolute error (MAE) into systematic and unsystematic components. PLoS One 2023;18:e0279774. [Crossref] [PubMed]
- Chai T, Draxler RR. Root mean square error (RMSE) or mean absolute error (MAE)? - Arguments against avoiding RMSE in the literature. Geoscientific Model Development 2014;7:1247-50. [Crossref]
- Brassington G. Mean absolute error and root mean square error: which is the better metric for assessing model performance? EGU General Assembly Conference Abstracts 2017.
- Karunasingha DSK. Root mean square error or mean absolute error? Use their ratio as well. Information Sciences 2022;585:609-29. [Crossref]
- Hodson TO. Root-mean-square error (RMSE) or mean absolute error (MAE): when to use them or not. Geoscientific Model Development 2022;15:5481-7. [Crossref]
- Charlier CVL. Grunddragen av den Matematiska Statistiken. Lund: Statsvetenskaplig Tidskrifts Expedition; 1910.
- Dahlberg G. Statistical methods for medical and biological students. London: G. Allen & Unwin Ltd.; 1940.
- Anderson TW, Darling DA. Asymptotic theory of certain "goodness of fit" criteria based on stochastic processes. Ann Math Statist 1952;23:193-212. [Crossref]
- Theodorsson E. BASIC computer program to summarize data using nonparametric and parametric statistics including Anderson-Darling test for normality. Comput Methods Programs Biomed 1988;26:207-13. [Crossref] [PubMed]
- Solberg HE. Approved recommendation (1987) on the Theory of Reference values. Part 5. Statistical treatment of collected reference values. Determination of reference limits. Clin Chim Acta 1987;170:S13-S32. [Crossref]
- Yap BW, Sim CH. Comparisons of various types of normality tests. Journal of Statistical Computation and Simulation 2011;81:2141-55. [Crossref]
- Solberg HE. The theory of reference values Part 5. Statistical treatment of collected reference values. Determination of reference limits. Clinica Chimica Acta 1984;137:95-114. [Crossref]
- Henny J. The IFCC recommendations for determining reference intervals: strengths and limitations. Laboratoriumsmedizin-Journal of Laboratory Medicine 2009;33:45-51. [Crossref]
- Box GEP, Cox DR. An analysis of transformations. J Royal Statistical Society Ser B 1964;26:211-43. [Crossref]
- Elveback LR, Taylor WF. Statistical methods of estimating percentiles. Annals of the New York Acadamy of Science 1969;161:538-48. [Crossref]
- Feinstein AR. X and Iprp - an Improved Summary for Scientific Communication. Journal of Chronic Diseases 1987;40:283-8. [Crossref] [PubMed]
- Patel JK, Read CB. Handbook of the normal distribution. Statistics, textbooks and monographs, vol 40. New York: M. Dekker; 1982.
- Liu RY, Tang J. Control charts for dependent and independent measurements based on bootstrap methods. Journal of the American Statistical Association 1996;91:1694-700. [Crossref]
- Faraz A, Heuchenne C, Saniga E. An exact method for designing Shewhart X and S2 control charts to guarantee in-control performance. International Journal of Production Research 2018;56:2570-84. [Crossref]
- Jones-Farmer LA, Woodall WH, Steiner SH, et al. An Overview of Phase I Analysis for Process Improvement and Monitoring. Journal of Quality Technology 2014;46:265-80. [Crossref]
- ISO. ISO/TS 20914:2019, Medical laboratories — Practical guidance for the estimation of measurement uncertainty. Geneva, Switzerland: International Organization for Standardization; 2019.
- Sadler WA. Imprecision profiling. Clin Biochem Rev 2008;29:S33-6. [PubMed]
- Berweger CD, Müller-Plathe F, Hänseler E, et al. Estimating imprecision profiles in biochemical analysis. Clin Chim Acta 1998;277:107-25. [Crossref] [PubMed]
- Sadler WA, Smith MH, Legge HM. A method for direct estimation of imprecision profiles, with reference to immunoassay data. Clin Chem 1988;34:1058-61. [Crossref] [PubMed]
- CLSI. EP15-A2 User Verification of Performance for Precision and Trueness. Approved Guideline Clinical and Laboratory Standards Institute; 2006.
- Aronsson T, Groth T. Nested control procedures for internal analytical quality control. Theoretical design and practical evaluation. Scand J Clin Lab Invest Suppl 1984;172:51-64. [PubMed]
- Kallner A. Laboratory Statistics: Methods in Chemistry and Health Sciences. Second edition. Amsterdam: Elsevier; 2018.
- Willmott CJ, Matsuura K, Robeson SM. Ambiguities inherent in sums-of-squares-based error statistics. Atmospheric Environment 2009;43:749-52. [Crossref]
- Thelen MHM, van Schrojenstein Lantman M. When bias becomes part of imprecision: how to use analytical performance specifications to determine acceptability of lot-lot variation and other sources of possibly unacceptable bias. Clin Chem Lab Med 2024;62:1505-11. [Crossref] [PubMed]
Cite this article as: Theodorsson E. Understanding and expressing variation in measurement results. J Lab Precis Med 2025;10:3.


